Ölçme Değişmezliği
Eğitimde sık sık grupları karşılaştırırız:
- kız–erkek,
- farklı sınıf düzeyleri,
- farklı sosyoekonomik düzeyler,
- şehir–köy,
- farklı okullar…
Bu karşılaştırmalar bize değerli bilgiler verir. Ama çok kritik bir soru çoğu zaman atlanır: “Bu iki grubu gerçekten aynı ölçme aracıyla adil biçimde karşılaştırabilir miyim?” İşte bu sorunun bilimsel yanıtı ölçme değişmezliği kavramında saklıdır.
Ölçme Değişmezliğinin Basit Tanımı
Ölçme değişmezliği bir ölçeğin farklı gruplarda aynı yapıyı aynı şekilde ölçmesi demektir. Bir ölçek hangi öğrenci grubu tarafından doldurulursa doldurulsun anlamını, boyutlarını, maddelerin işleyişini değiştirmemelidir. Örneğin “matematik kaygısı” ölçeği hem kızlarda hem erkeklerde gerçekten matematik kaygısını ölçüyorsa değişmezlik vardır. Yoksa, bir grupta “kaygı” olarak okunan madde diğer grupta “özgüven eksikliği” olarak yorumlanıyorsa orada karşılaştırma bilimsel olarak geçersiz hale gelir.
Neden Ölçme Değişmezliği Bu Kadar Önemlidir?
Çünkü karşılaştırmalar ancak ölçme değişmezliği sağlandığında anlamlı olur. Örneğin kız ve erkek öğrencilerin matematik kaygısını karşılaştırıyorsunuz. Ölçekteki bazı maddeler kızlar için daha duygusal bir anlam taşıyor erkekler için daha nötr bir ifade gibi algılanıyor olabilir. Bu durumda iki grup arasındaki fark gerçek kaygı farkı değildir maddelerin işleyişi farkı olabilir.
Ölçme değişmezliği sağlanmadan yapılan grup karşılaştırmaları:
- hatalı politika kararlarına,
- yanlış yönlendirmelere,
- adil olmayan yorumlara,
- öğrenciler hakkında yanlış sonuçlara yol açabilir.
“Matematik dersine yönelik tutum ölçeği” uyguladığınızı düşünün. Ölçekte şu madde var: “Matematik dersinde soru çözerken geriliyorum.” Bu madde:
- Bir grup için performans kaygısını,
- Başka bir grup için özgüven eksikliğini,
- Başka bir grup için konu eksikliğini
akla getiriyorsa ölçek her grupta farklı şeyi ölçüyor olabilir. Bu durumda elde ettiğiniz sayısal farkların hangi yapıyı temsil ettiği belirsizdir. İşte ölçme değişmezliği bu belirsizliği ortadan kaldırır.
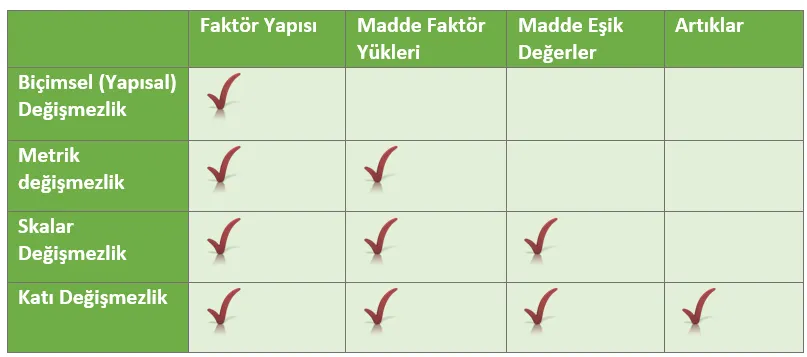
Ölçme Değişmezliğinin Üç Düzeyi
1. Yapı Değişmezliği (Configural Invariance)
Soru: “Ölçeğin boyut yapısı aynı mı?” Örneğin:
- Kızlarda 2 boyut erkeklerde 3 boyut çıkıyorsa → değişmezlik yoktur.
Bu aşamada sadece şu kontrol edilir: Ölçeğin genel mimarisi gruplar arasında aynı görünüyor mu?
2. Metri̇k Değişmezlik (Factor Loading Invariance)
Soru: “Maddeler yapıya aynı güçte mi bağlanıyor?” Yani bir madde kızlarda daha güçlü erkeklerde daha zayıf bağlanıyorsa:
- Maddeler aynı türde bilgi üretmiyor demektir.
- Ölçeğin toplam puanı iki grup için farklı anlam taşır.
Bu aşama “ölçek madde madde aynı çalışıyor mu?” sorusunu yanıtlar.
3. Skalar Değişmezlik (Scalar Invariance)
“Aynı düzeydeki öğrenciler aynı puanı alıyor mu?” ölçme değişmezliğinin en kritik aşamalarından biridir. Bir örnekle açıklayalım: Kız ve erkek öğrenciler matematik kaygısı bakımından gerçekte aynı düzeyde olsun. Ama ölçekte kızlar daha yüksek puan alıyor erkekler daha düşük puan alıyorsa… Üstelik bu fark gerçek kaygı düzeyinden değil ölçeğin işleyişinden kaynaklanıyorsa… İşte bu skalar değişmezliğin bozulduğunu gösterir. Skalar değişmezlik sağlandığında: “Aynı yetenekteki her öğrenci aynı puanı alır.”
Bu aşama gruplar arasında gerçek ortalama farkı olup olmadığını test etmeyi mümkün kılar.
4. Katı Değişmezlik (Strict Invariance)
“Ölçüm hatası tüm gruplarda aynı mı?” ölçme değişmezliğinin en kapsamlı ve en sıkı aşamasıdır. Burada şunlara bakılır:
-
Ölçeğin hata payı her grupta aynı mı?
-
Puanlayıcı etkisi (özellikle performans puanlarında) aynı mı?
-
Maddelerin hata varyansları eşit mi?
Katı değişmezlik sağlandığında ölçeğin “gruplar arası karşılaştırma” kapasitesi en üst düzeye çıkar. Bu aşama sağlanmışsa şu mesaj verilir: “Bu ölçeğin hem yapısı hem maddeleri hem de hata payı gruplar arasında aynı şekilde çalışıyor.” Katı değişmezlik özellikle büyük ölçekli sınavlar, uzunlamasına izleme çalışmaları ve politika düzeyindeki karşılaştırmalar için ideal düzeydir.
DIF ile İlişkisi
Bu iki kavram birlikte anılır ama aynı şey değildir.
| Kavram | Açıklama |
|---|---|
| DIF (Madde İşlev Farklılığı) | Tek tek maddelerin adil çalışıp çalışmadığını inceler. |
| Ölçme Değişmezliği | Ölçeğin bütün yapısının farklı gruplarda aynı olup olmadığını test eder. |
Kısacası:
DIF = maddelere bakar
Ölçme değişmezliği = yapıya bakar
Ölçme değişmezliği bozulduğunda genelde maddelerde DIF de vardır.
Ölçme Değişmezliği Sağlanmazsa Ne Yapılır?
Burada öğretmene düşen üç kritik adım vardır:
-
Probleme neden olan maddeler belirlenir.
-
Bu maddeler dilsel olarak sadeleştirilir veya bağlamı değiştirilir.
-
Gerekirse madde çıkarılır ve ölçek yeniden test edilir.
Araştırmacılar bu süreç için DIF analizi, faktör analizi ve uyum indeksleri gibi araçlar kullanır.
Ölçme Değişmezliği Adaletin ve Bilimsel Karşılaştırmanın Şartıdır
Grupları karşılaştırmak güçlü bir araçtır… Ama yalnızca ölçme değişmezliği sağlanmışsa. Özetle şunu söyleyebiliriz: Ölçme değişmezliği, farklı grupların aynı ölçekle adil biçimde karşılaştırıldığının bilimsel güvencesidir. Aksi durumda sayısal farklar bir gerçeği değil ölçme aracının hatasını gösterebilir. Bu yüzden “ölçme değişmezliği” sadece araştırmacılar için değil okul yöneticileri ve öğretmenler için de temel bir ölçme okuryazarlığı konusudur.